Fakty, fikcja i dostosowanie – Donald Hoffman i inni
Źródło: Fact, Fiction, and Fitness, Entropy 2020, 22(5), 514 https://www.mdpi.com/1099-4300/22/5/514

Teoria świadomości – niezależnie od innych zagadnień, którymi się zajmuje – musi odnosić się do struktury doświadczenia. Nasze doświadczenia percepcyjne mają bogatą budowę. Zwyczajne przyglądanie się czerwonemu jabłku, kołyszącemu się wśród zielonych liści na potężnym drzewie, wiąże się z symetriami, geometriami, porządkami, topologiami i algebrami zdarzeń. Czy struktury te są także obecne na świecie, w pełni niezależne od tego czy się je obserwuje? Teoretycy percepcyjni wielu ruchów – od algorytmicznego do radykalnie ucieleśnionego – odpowiadają: percepcja prawdziwie przedstawia obserwatorom struktury, które istnieją w świecie niezależnym od obserwatora, a dzieje się tak, ponieważ dobór naturalny kształtuje systemy percepcyjne w taki sposób, aby były coraz bardziej prawdziwe. W niniejszym opracowaniu badamy cztery struktury: całkowite porządki, grupy permutacji, grupy cykliczne oraz przestrzenie mierzalne. Stawiamy pytanie czy funkcje wypłaty, które napędzają ewolucję na drodze doboru naturalnego są homomorfizmami tych struktur. Udowadniamy, w każdym przypadku, że ogólnie odpowiedź brzmi nie: podczas gdy liczba stanów w świecie i wartości wypłaty ciągnie się w nieskończoność, prawdopodobieństwo, że funkcje wypłaty są homomorfizmami spada do zera. Wyciągamy wniosek, że dobór naturalny niemal na pewno kształtuje sposoby postrzegania tych struktur tak, że są one nieprawdziwe. Jest to zgodne z teorią percepcji jako interfejsu, która głosi, że dobór naturalny kształtuje systemy percepcyjne w taki sposób, aby nie zapewniały prawdziwego postrzegania, ale by służyły jako interfejsy konkretne dla danego gatunku, które kierują zachowaniem adaptacyjnym. Uzyskane przez nas wyniki stanowią ograniczenie każdej teorii świadomości, która zakłada, że struktura w doświadczeniu percepcyjnym kształtowana jest przez dobór naturalny.
[Homomorfizm – przekształcenie dowolnego systemu algebraicznego w inny system algebraiczny, zachowujące odpowiadające sobie działania oraz wyróżnione elementy.]
Czy widzimy rzeczywistość taką, jaka ona jest – Donald Hoffman
Teoria ‘Dostosowanie Przebija Prawdę’ – Donald Hoffman
Konieczne kłamstwa, proste prawdy – Daniel Goleman
1. Wstęp
Jeżeli świat doświadczany przez noworodka jest chaotyczny, „wielkie, kwitnące, tętniące życiem zamieszanie”, świat dorosłego z pewnością taki nie jest. Na przykład świadomie doświadczana przestrzeń wizualna posiada geometrię nieeuklidesową[1,2,3,4]. Analizy formalne doświadczeń kolorów dostarczają bogactwa struktur takich jak sześcian RGB, bryła barw Schrödingera, kolektory ssące, wiązki włókniste oraz przestrzeń barw CIEXYZ[5,6]. Przedmioty i powierzchnie doświadczane wizualnie dopuszczają opis za pomocą geometrii różniczkowej[7,8,9]. Doświadczenia intensywności dźwięku uporządkowane są od cichego do głośnego; ton uporządkowany jest od niskiego do wysokiego.
KOLOR – program wiedzy społecznej
To oczywiście żadna niespodzianka. Struktura doświadczenia jest tematem eksperymentów co najmniej od przełomowego dzieła fizjologa Ernsta Heinricha Webera w latach 30-tych XIX wieku. Badania te połączyły się tworząc dziedzinę naukową wraz z publikacją w 1860 roku książki „Elements of Psychophysics” autorstwa fizyka i filozofa Gustava Theodora Fechnera. Celem psychofizyki jest zbadanie struktur doświadczenia oraz ich związku ze strukturami świata fizycznego. Jak wyjaśniają Duncan Luce i Carol Krumhansl[10]:
[Psychofizyka] przewiduje odkrycie ogólnych praw odnoszących doznania do właściwości fizycznych. Oznacza to, że oczekuje się, iż mierzone doznania będą odpowiadać w sposób uporządkowany wielkościom fizycznym, które dają im początek.
Zakłada się, że uporządkowane odpowiedniki wywnioskowane z doświadczeń psychofizycznych, które można przedstawić formalnie jako mapy od obserwowanego świata do świadomych doświadczeń osoby postrzegającej zmysłami, to homomorfizmy. Homomorfizm to odwzorowanie na mapie, które wiernie przenosi strukturę, I, właściwości fizycznej świata do struktury Ψ(I) doznań. Dla przykładu właściwość fizyczna I, amplituda akustycznego ciśnienia atmosferycznego, ma strukturę całkowitego porządku od niskiej amplitudy do wysokiej amplitudy. Analogiczne doznanie natężenia dźwięku Ψ(I) to również całkowity porządek od niskiej do wysokiej amplitudy. Powiązanie między nimi w typowym zakresie częstotliwości ludzkiego układu słuchowego to prawo potęgowe: Ψ(I)=kIα(f) (tutaj α(f)=0.67 dla dźwięku o częstotliwości 3000 Hertzów, zaś k zależy od użytych jednostek. Mapa ta przenosi lub respektuje całkowity porządek: jeśli amplituda akustyczna i1 jest większa niż i2, wówczas postrzegane natężenie dźwięku Ψ(i1) jest większe niż Ψ(i2) pod warunkiem, że pozostaje w zakresie ludzkiej częstotliwości akustycznej. Ta forma prawa potęgowego, zwana potęgowym prawem Stevensa na cześć psychofizyka Stanley’a Stevensa, odnosi się do mnogości doznań, w tym wibracji, jaskrawości, jasności, długości wizualnej, powierzchni wizualnej, ciepła, bólu, namacalnej szorstkości i twardości, ciężaru oraz wstrząsu elektrycznego (analiza krytyczna: patrz[11,12]). Wykładnik potęgi w prawie potęgowym zależy rzecz jasna od doznania. Jednak w każdym przypadku mapa od właściwości fizycznych świata do doznań jest także, w typowym zakresie dynamicznego odpowiedniego systemu detekcji człowieka, homomorfizmem.
Nie jest to kwestia pomniejszej wagi. Psychofizyka zakłada istnienie świata niezależnego od obserwatora i co więcej takiego, którego strukturę i funkcję opisuje fizyka, nawet jeśli nie postrzega go żadna żywa istota. Założenie to wymownie ilustruje słynne pytanie dotyczące teorii kwantowej, które Einstein zadał Abrahamowi Paisowi. Pais przypomina sobie, że Einstein zapytał „czy naprawdę wierzę, że księżyc istnieje tylko wtedy, gdy na niego patrzę” [13]. Jeżeli zmysł ma nas informować zgodnie z rzeczywistością o takim niezależnym od obserwatora świecie (ang. OIW, observer-independent world), wówczas mapa od OIW do doświadczeń generowanych przez ten zmysł pod żadnym pozorem nie może pomieszać ani wymazać tej struktury. Zmysł może nas informować o strukturze świata niezależnego od obserwatora [OIW] tylko w takim stopniu, w jakim mapa zbliża się do homomorfizmu. Jeśli zmysłowi uda się poinformować nas o strukturze świata niezależnego od obserwatora [OIW], wynikające z tego postrzeganie nazywane jest „prawdziwym”. Prawdziwość w tym znaczeniu to „prawda” w tradycyjnym sensie korespondencyjnej teorii prawdy, według której zdanie jest prawdziwe, jeżeli relacjonuje stan faktyczny świata niezależnego od obserwatora[14]. To założenie prawdziwości jest standardowe w naukach percepcyjnych i kognitywnych. Wyjaśnia to między innymi fakt, że standardowo uznaje się, iż percepcja wizualna wprowadza w życie „odwróconą optykę” – konkretnie traktuje się ją jako proces, który szacuje najbardziej prawdopodobną strukturę świata 3D, odpowiedzialną za generowanie jakichkolwiek obrazów rzeczywistych na siatkówce 2D[15,16].
Psychofizyka zakłada, że „zmienne fizyczne”, w tym intensywność światła, amplituda akustyczna itd., stanowią obiektywne komponenty świata niezależnego od obserwatora [OIW] i z tego powodu opisy OIW oparte na bezpośrednich pomiarach tych fizycznych zmiennych dostarczają „prawdę podstawową”, którą można zastosować do potwierdzenia zasadności mniej bezpośrednich pomiarów. W tym przypadku dowody empiryczne odwzorowań psychofizycznych (takich jak potęgowe prawo Stevensa) od zmiennych fizycznych do doświadczanych wielkości lub innych rezultatów stanowią dowód, że takie doświadczenia są homomorficzne wobec struktur w świata niezależnego od obserwatora i tym samym są prawdziwe. Jednakże można również twierdzić, że to, co nazywamy zmiennymi fizycznymi jest samo w sobie wynikiem procedur pomiarów, które wykonują obserwatorzy wykorzystując swoje własne systemy percepcyjne i pojęciowe i, co więcej, że wyniki tych pomiarów wyrażone są albo w kategoriach predykatów, którymi posługują się nasze wyobrażenia percepcyjne albo jako proste uogólnienia takich predykatów[17,18]. Jeśli tak, odwzorowania psychofizyczne wskazują po prostu na podobieństwo systematyczne między dwiema różnymi postaciami „pomiarów”, których dokonują obserwatorzy – bezpośrednie pomiary „fizyczne” (często wprowadzane w życie za pomocą określonej aparatury mierniczej) i mniej bezpośrednie pomiary „percepcyjne”. Analogie te są niebagatelne i ciekawe; stanowią jednak homomorficzne mapy między różnymi doświadczeniami percepcyjnymi, nie zaś mapy homomorficzne pomiędzy doświadczeniami percepcyjnymi a światem niezależnym od obserwatora. Powrócimy do tej kwestii odpowiadając na zastrzeżenia w §5.
Nawet pomimo że teorie percepcji (zarówno w ramach nauk, jak i filozofii umysłu) uznają, iż prawdziwość wymaga odwzorowań homomorficznych między światem niezależnym od obserwatora a naszymi doświadczeniami, z większości tych teorii wynika, że niektóre nasze spostrzeżenia mogą być prawdziwe i że możemy za to podziękować doborowi naturalnemu. Zgadzają się w tej kwestii, nawet jeśli nie są zgodne w innych podstawowych sprawach takich jak pytanie czy percepcja wiąże się z wyobrażeniem czy z wyliczeniem.
Przykładowo neurofizjolog David Marr twierdził, że „nasze przetwarzanie percepcyjne zwykle naprawdę działa właściwie (zapewnia prawdziwy opis tego, co istnieje)”[19]. Przypisywał ten sukces doborowi naturalnemu, utrzymując, że my:
„Z całą pewnością faktycznie wyliczamy jednoznaczne właściwości istniejących, rzeczywistych, widzialnych powierzchni, zaś jednym z interesujących aspektów ewolucji systemów wizualnych jest stopniowe przesuwanie się w stronę trudnego zadania progresywnego przedstawiania bardziej obiektywnych aspektów świata wizualnego.”
„Obiektywny” oznacza tutaj niezależny od jakiegokolwiek obserwatora lub obserwacji: „obiektywny aspekt świata wizualnego” to struktura bądź stan świata niezależnego od obserwatora. Filozof Jerry Fodor stanowczo twierdził, że[20]:
„Nie ma niczego w „ewolucyjnym” lub „biologicznym” czy też „naukowym” spojrzeniu na świat, co pokazywałoby ani nawet sugerowało, że właściwą funkcją poznania jest coś innego niż utrwalanie prawdziwych przekonań.”
Fodor używa tu słowa „prawdziwe” w kontekście analogii, o której była mowa powyżej. Naukowiec kognitywny Zygmunt Pizlo zgadza się, że[21]:
„Prawdziwość jest konieczną właściwością percepcji i poznania. Jest absolutnie niezbędna. Percepcja i poznanie bez prawdziwości byłyby jak fizyka bez praw zachowania.”
Każdy z tych teoretyków sugerował, że systemy percepcyjne przetwarzają informacje i że prawdziwość uzyskuje się częściowo poprzez zaawansowane obliczenia. Orędownicy poznania ucieleśnionego odrzucają tę sugestię w jej miejsce twierdząc, że dobór naturalny osiąga prawdziwość kształtując połączoną dynamikę organizmu i środowiska. Filozof i naukowiec kognitywny Anthony Chemero twierdzi na przykład, że[22]:
„Okej, więc (radykalni) naukowcy reprezentujący nurt poznania ucieleśnionego mogą być realistami. Oznacza to, iż mogą wierzyć, że istnieje świat niezależny od zwierząt i że niektóre nasze spostrzeżenia są wyrazem tego, iż dobrze go rozumieją.”
Podobnie filozof Alva Noë i psycholog Kevin O’Regan wnioskują, że „Obserwatorzy nie mylą się uważając, że mają dostęp do szczegółów związanych ze środowiskiem”[23].
W dalszej części dokładnie zbadamy twierdzenie, że struktura świadomego doświadczenia jest, przynajmniej przez jakiś czas, homomorficzna wobec budowy domniemanego świata niezależnego od obserwatora [OIW] i dlatego też można ją uznać, przynajmniej przez jakiś czas, za prawdziwą w trwałym sensie, jakiego wymaga korespondencyjna teoria prawdy. Rozważymy zdecydowanie najbardziej rozpowszechniony argument na rzecz prawdziwości: że dobór naturalny w czasie ewolucyjnym przywodzi systemy percepcyjne organizmów do czegoś, co jest przynajmniej w przybliżeniu prawdziwością. Formułujemy ten argument w kategoriach ewolucyjnej teorii gier i dowodzimy, że przy uwzględnieniu założeń generycznych prawdopodobieństwo, iż funkcje wypłaty wynikającej z dostosowania są homomorfizmami określonych struktur w świecie zbliża się do zera, podczas gdy liczba możliwych stanów w świecie i potencjalnych wartości wypłaty staje się znacząca.
Rozpatrywane tu struktury to całkowite porządku, grupy permutacji, grupy cykliczne oraz przestrzenie mierzalne. Struktury te są kluczowe dla odpowiednio postrzegania wielkości (np. głośności, twardości lub ciepła zgodnie z tym, co powiedziano wcześniej), zmian ustawienia przedmiotów oraz rozkładu prawdopodobieństwa. Jako że zarówno geometria euklidesowa, jak i układna geometria nieeuklidesowa, w tym doświadczana geometria przestrzeni wizualnej, szanują inwarianty obrotowe oraz inwarianty translacji, struktury wprowadzane w życie przez grupy cykliczne są w szczególności kluczowe dla prawdziwej percepcji przestrzeni geometrycznej. Te cztery twierdzenia, które udowadniamy, dotyczą informacji o wspomnianych strukturach, udostępnionych obserwatorom przez funkcje wypłaty wynikającej z dostosowania. Twierdzenia te są niezależne od jakichkolwiek konkretnych założeń dotyczących obserwatorów lub ich struktur, w szczególności od poziomu i skali organizacyjnej (np. zgodnie z definicją w [24,25]), na której zachodzi dobór.
Wyniki te pokazują, że jeśli nie wprowadzi się nowatorskich, silnie restrykcyjnych (i niewracających do punktu wyjścia) założeń na temat struktur funkcji wypłaty wynikającej z dostosowania, odwołania do doboru naturalnego nie będą wspierać twierdzeń dotyczących prawdziwych doświadczeń. To, że percepcja ma ograniczony zasięg jest dobrze rozumiane. Dla przykładu światło, które widzą ludzie pochodzi wyłącznie z cienkiego pasma spektrum elektromagnetycznego. Przedstawione przez nas twierdzenia pokazują, że nasza percepcja nie jest prawdziwa nawet w tym ograniczonym zakresie, w którym faktycznie działa, tj. nigdy wiernie nie relacjonuje struktur w świecie niezależnym od obserwatora nawet w ramach tych ograniczeń. Wyniki są zgodne z teorią percepcji jako interfejsu (ang. ITP, interface theory of perception[17,18,26]), zgodnie z którą dobór naturalny kształtuje systemy percepcyjne, aby wykształciły interfejs określony dla danego gatunku, który będzie kierował zachowaniem adaptacyjnym, nie zaś po to, by zapewniły prawdziwe doświadczenia obiektywnej rzeczywistości. Jako takie wyniki stanowią ograniczenie jakiejkolwiek teorii świadomości, która zakłada, że struktura w doświadczeniu percepcyjnym kształtowana jest przez dobór naturalny.
2. Dobór naturalny
Argumenty na poparcie prawdziwej percepcji, jak stwierdzono powyżej, opierają się często na doborze naturalnym. Podstawowa koncepcja głosi, że ci z naszych poprzedników, którzy postrzegali świat niezależny od obserwatora [OIW] w bardziej dokładny sposób mieli przewagę konkurencyjną nad tymi, którzy postrzegali go mniej precyzyjnie i z tej przyczyny było bardziej prawdopodobne, że staną się naszymi przodkami, przekazując geny, które kodowały dokładniejsze systemy sensoryczne. Jesteśmy potomstwem takich przodków, a więc mamy powód, by żywić pewność, że nasza percepcja jest w normalnym sytuacji prawdziwa.
Psycholog Stephen Palmer ujmuje ten argument zwięźle: „Mówiąc z perspektywy ewolucji, percepcja wizualna jest użyteczna jedynie, jeśli jest wystarczająco precyzyjna”[27]. Teoretyk ewolucji Robert Trivers twierdzi[28]:
„Nasze systemy sensoryczne są tak zorganizowane, by dać nam szczegółowy i precyzyjny obraz rzeczywistości dokładnie tak, jak byśmy się tego spodziewali, gdyby prawda o świecie zewnętrznym pomagała nam skuteczniej odnajdywać w nim drogę.”
Podobnie psycholog Roger Shepard sugeruje, że ewolucja ukształtowała nasze zmysły, by internalizować rozmaite prawidłowości świata zewnętrznego. W swoim artykule „Perceptual-cognitive universals as reflections of the world” utrzymuje[29]:
„Dobór naturalny gwarantuje (w warunkach sprzyjających percepcji), że ogólnie rzecz biorąc postrzegamy przemianę, którą obiekt zewnętrzny tak naprawdę przechodzi w świecie zewnętrznym, jakkolwiek jest ona prosta czy złożona, ścisła czy też łagodna.”
Warto tu zauważyć, że założenie świata niezależnego od obserwatora leży u podstaw wszystkich tych twierdzeń.
Jednakże niektórzy się z tym nie zgadzają, twierdząc, że dobór naturalny nie sprzyja prawdziwej percepcji. Filozof Patricia Churchland twierdzi natomiast, że[30]:
„Jeśli się na niego spojrzy z ewolucyjnego punktu widzenia, główną funkcją układu nerwowego jest […] rozmieszczenie części ciała tam, gdzie być powinny po to, żeby organizm mógł przetrwać […] Prawda, czymkolwiek by nie była, zupełnie się nie liczy.”
Zgadza się z tym naukowiec kognitywny Steven Pinker[31]:
„Nasze umysły wykształciły się na drodze doboru naturalnego po to, aby rozwiązywać problemy, które były sprawami życia i śmierci dla naszych przodków, a nie po to, by obcować z poprawnością.”
Później jednak przyznaje, że „faktycznie mamy jakieś wiarygodne pojęcie o rozmieszczeniu wokół nas przedmiotów średniej wielkości” [32]. Obecnie powszechna jest wiedza, że główne siły selektywne w ewolucji człowieka są społeczne[33]. Dlatego też „światem”, do którego przystosowuje się ludzka percepcja jest nie tylko domniemany świat niezależny od obserwatora, ale jest nim też świat innych doświadczających organizmów. Podczas gdy niejednokrotnie wyraźnie uznaje się społeczny charakter ludzkiego świata (czyni to np. Trivers[28]), świat niezależny od obserwatora jest nadal uważany za „prawdę podstawową” przez teoretyków mówiących o prawdziwej percepcji.
Mamy tu sytuację patową. Teoretycy wykorzystują dobór naturalny, by argumentować zarówno na rzecz, jak i przeciwko prawdziwej percepcji. A zatem który argument jest prawidłowy? Zakładając, że dobór naturalny steruje ewolucją systemów percepcyjnych, nie musimy spekulować czy sprzyja to prawdziwemu postrzeganiu. Możemy dowodzić twierdzeń. W kolejnej części dokonujemy przeglądu podstawowych koncepcji potrzebnych do tego, by zrozumieć te twierdzenia i ich nadzwyczajne implikacje.
3. Gry ewolucyjne
Teorię Darwina można przedstawić za pomocą precyzyjnego sformułowania w matematyce ewolucyjnej teorii gier[34]. Pomocne w zrozumieniu gier ewolucyjnych jest wyobrażenie sobie gry video, w której gracz zdobywa punkty. Nagrodą jest przejście na kolejny poziom gry. Gracz ma dostęp do wielu rozmaitych strategii, m.in. może wybierać narzędzia i taktykę.
Gracze w grach ewolucyjnych mogą rywalizować stosując różne strategie, aby zdobyć nagrody za dostosowanie; w istocie najbardziej interesujące gry to te, w których wykorzystuje się różnorodne strategie z jednakową zręcznością. Strategię, która przeciętnie przynosi większą nagrodę niż strategie konkurencyjne nazywa się bardziej dostosowaną. Nagrodą jest reprodukcja – nowa generacja, w której więcej graczy używa tej strategii. Podczas gdy „ewolucję” postrzega się jako metodę optymalizacji w poszukiwaniach opartych na algorytmie genetycznym[35,36], ewolucja biologiczna jest jedynie zadowalająca[37,38]. Odzwierciedleniem tego w ewolucyjnej teorii gier jest założenie przypadkowej funkcji wypłaty której przeciwieństwo stanowi funkcja miar dopasowania z celem a priori[34,39].
Jednak korzyści wynikające z dostosowania zależą w dużej mierze od kontekstu. Rozważmy je na przykładzie liście eukaliptusa. Głodnemu koali chcącemu jeść oferują pożywienie. Najedzonemu koali, który chce się połączyć w parę nie oferują niczego. Głodnemu człowiekowi, który chce jeść oferują śmierć na skutek spożycia cyjanku. Najedzonemu człowiekowi, który chce się połączyć w parę nie oferują niczego. Te same liście oferują szalenie różne nagrody w zależności od organizmu (koala versus człowieka), jego stanu (głodny versus najedzony) oraz czynności (jedzenie versus łączenie się w parę). Kluczowe jest tu zrozumienie, że korzyści wynikające z dostosowania zależą od łącznego stanu świata niezależnego od obserwatora – w tym przykładzie liści – oraz zamieszkującego/cych go obserwatora/ów: w tym przypadku zwierząt, ich stanów i wykonywanych przez nie czynności.
Domeną „globalnej funkcji dostosowania” byłby zatem nie tylko niezależny od obserwatora świat W, ale kartezjański iloczyn W×O×S×A, gdzie O to grupa organizmów, S to ich potencjalny stan, zaś A to ich możliwa kategoria czynności. Kiedy ustalimy konkretny organizm o∈O, stan s∈S i kategorię czynności, otrzymamy określoną funkcję dostosowania fo,s,a, zdefiniowaną w świecie W [17,18,40].
Możemy zatem efektywnie przedstawić wynikającą z tego (określoną) funkcję wypłaty wynikającej z dostosowania za pomocą funkcji, która odzworowuje stany świata niezależnego od obserwatora, w∈W, pod postacią wartości wypłaty v∈V. Tym samym, dla ustalonego organizmu i kategorii czynności oraz po zablokowaniu parametrów o,s i a, otrzymujemy funkcję:
f:W→V.
(1)
Powyższe funkcje wypłaty napędzają ewolucję poprzez dobór naturalny. Kształtują percepcję oraz działanie. Determinują czy dobór naturalny sprzyja prawdziwemu postrzeganiu.
Zilustrujemy to prostym przykładem. Przykład ten służy także temu, by podkreślić istotną kwestię, mianowicie że między korzyściami wynikającymi z dostosowania a prawdziwością w odniesieniu do struktury świata (niezależnego od obserwatora) nie musi istnieć korelacja. Przypomnijmy sobie, że właściwym tutaj wyobrażeniem prawdziwości (i tym, które standardowo zakłada się w naukach percepcyjnych i kognitywnych) jest w istocie prawdziwość w odniesieniu do struktury świata (niezależnego od obserwatora) (patrz Część 1). Załóżmy, że świat posiada zasoby, nazwijmy je surowcami, oraz żyje na nim stworzenie, nazwijmy je istotą żywą, które je surowce. Istoty żywe widzą tylko dwa kolory, jasnoszary i ciemnoszary. Kiedy istoty żywe szukają pożywienia, decydują co zjeść kierując się kolorami, które widzą. Załóżmy, że funkcja wypłaty przypisuje większe wartości większej ilości surowców, jak widać na Ilustracji 1. Rozważmy istotę żywą, która widzi kolor jasnoszary, jeśli jest dużo surowców i ciemnoszary, jeśli jest inaczej, jak to pokazuje Ilustracja 1b. Mapa sensoryczna istoty żywej to homomorfizm całkowitego porządku – jaśniejszy kolor odpowiada większej ilości surowców. Tym samym jego percepcja jest prawdziwa: zachowuje strukturę porządku surowców na świecie. Ta istota żywa korzysta z prostego sposobu, by zebrać więcej nagród: je tam, gdzie widzi kolor jasnoszary. Weźmy pod uwagę inną istotę żywą, która widzi kolor jasnoszary, jeśli ilość jest średnia i ciemnoszary, jeżeli jest inaczej, jak to pokazano na Ilustracji 1c. Jej mapa sensoryczna nie jest homomorfizmem całkowitego porządku – ciemniejszy kolor odpowiada większej ilości surowców i mniejszej ilości surowców. Jej percepcja nie jest prawdziwa: miesza strukturę porządku surowców na świecie. Ta istota żywa nie ma możliwości zebrania większej liczby nagród. Jeżeli je tam, gdzie widzi kolor ciemnoszary, niekiedy trafia jej się dużo surowców, a innym razem niewiele. Jest mniej dostosowana niż prawdziwa istota żywa.

Ilustracja 1. Podział korzyści wynikających z dostosowania: (a) Korzyść wynikająca z dostosowania to funkcja liniowa ilości surowców. (b) „Prawdziwa” mapa sensoryczna, która jest homomorficzna dla tej funkcji. (c) „Nieprawdziwa” mapa sensoryczna, która nie jest homomorficzna dla tej funkcji. Jest mniej dostosowana niż mapa sensoryczna przedstawiona w (b).
Zamiast tego załóżmy, że funkcja wypłaty przypisuje większe wartości średniej ilości surowców, jak widać na Ilustracji 2. Teraz prawdziwa istota żywa jest w tarapatach. Nie ma możliwości, aby stale zbierała więcej nagród. Jeśli je tam, gdzie widzi kolor jasnoszary, czasami dostaje dużą nagrodę, a innym razem małą. Napotyka ten sam problem, jeśli żywi się tam, gdzie widzi kolor ciemnoszary. Jednakże nieprawdziwa istota żywa w prosty sposób zbiera duże nagrody: je tam, gdzie widzi kolor jasnoszary.
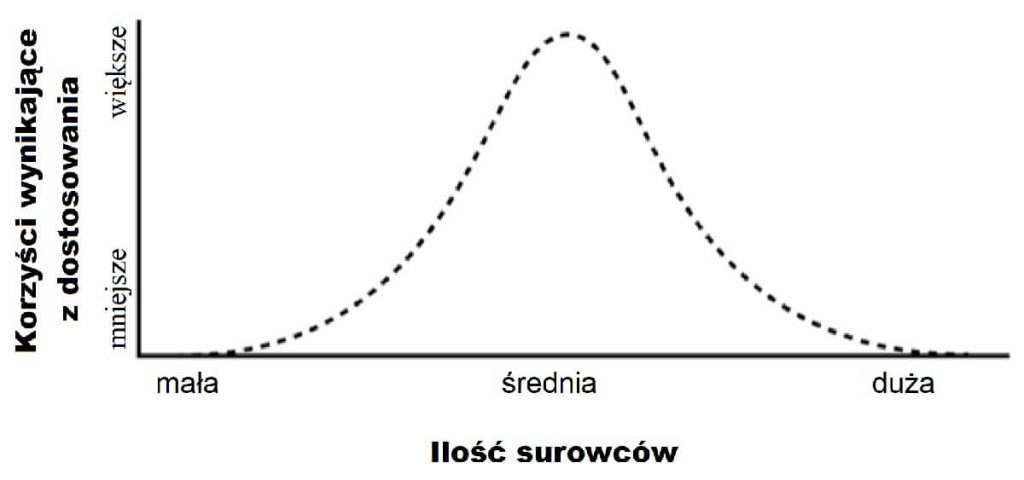
Ilustracja 2. Funkcja wypłaty, która jest funkcją nieliniową ilości surowców. Teraz nieprawdziwa mapa sensoryczna na Ilustracji 1c byłaby bardziej dostosowana niż mapa sensoryczna na Ilustracji 1b.
Co spowodowało tę różnicę? Kluczowe jest to czy funkcja wypłaty sama w sobie jest homomorfizmem struktury w świecie. Jeżeli jest, jak pokazano na Ilustracji 1, wówczas prawdziwa percepcja jest bardziej dostosowana i dobór naturalny jej sprzyja. Jeśli nie jest, jak przedstawiono na Ilustracji 2, wówczas prawdziwa percepcja nie jest bardziej dostosowana [przydatna]. Zamiast tego bardziej dostosowane jest nieprawdziwe postrzeganie, które jest homomorfizmem funkcji wypłaty i to jemu sprzyja dobór naturalny[42,44]. A zatem to czy funkcja dostosowania jest czy też nie jest homomorfizmem decyduje o tym czy potrafi wesprzeć prawdziwe doświadczenia – te, które zachowują strukturę w niezależnym od obserwatora świecie W.
Co z funkcjami wypłaty, które nie są homomorfizmami struktury w świecie? Czy naprawdę mogą wystąpić? Czy są po prostu abstrakcyjnymi i nieprawdopodobnymi możliwościami? Tak się składa, że występują często. Weźmy pod uwagę tlen. Jego zbyt mała lub zbyt duża ilość jest dla nas zgubna. Jedynie wąski zakres częściowego ciśnienia tlenu, pomiędzy 19,5% a 23,5%, można utrzymać nas przy życiu. Tak więc funkcja wypłaty nie jest tu homomorfizmem: zarówno niski, jak i wysoki poziom tlenu łączy się z niskimi wartościami dostosowania, podczas gdy wartości średnie łączą się z wysokimi wartościami dostosowania. To samo odnosi się do promieniowania ultrafioletowego, poziomu glukozy we krwi i całego mnóstwa innych przykładów. Nie jest to żadnym zaskoczeniem. Życie jest delikatne i wymaga restrykcyjnego zachowywania homeostazy. A zatem odpowiednie funkcje wypłaty nie są homomorfizmami całkowitych porządków.
Zawartość tlenu w powietrzu w masce – Jeff Neff [strażak]
Może się zdarzyć, że funkcje wypłaty nie będą homomorfizmami. Ale czy to prawdopodobne? Jeśli tak, możliwe, że dobór będzie faworyzować nieprawdziwość; jeśli nie, prawdopodobnie wesprze prawdziwość. Jeżeli potrafimy zdecydować o prawdopodobieństwie, że funkcje wypłaty są homomorfizmami, wówczas jesteśmy w stanie zdecydować o prawdopodobieństwie, że nasza percepcja jest prawdziwa.
Na tym koncentruje się niniejsze opracowanie. Obliczamy prawdopodobieństwo, że funkcje wypłaty są homomorfizmami dla czterech rodzajów struktur: całkowitych porządków, grup permutacji, grup cyklicznych oraz przestrzeni mierzalnych. Mówi nam to z jakim prawdopodobieństwem postrzegamy te struktury prawdziwie. Odpowiedź w każdym przypadku jest taka sama: prawdopodobieństwo prawdziwej percepcji jest zerowe.
Wyliczamy te prawdopodobieństwa za pomocą działań. Liczymy wszystkie możliwe funkcje wypłaty i wszystkie funkcje wypłaty, które są homomorfizmami. Dzielimy liczbę homomorfizmów przez całkowitą liczbę możliwych funkcji wypłaty, aby otrzymać prawdopodobieństwo. (Dla większej ostrożności w rzeczywistości liczymy tylko całkowitą liczbę „dopuszczalnych” funkcji dostosowania – tych, które osiągają maksymalne dostosowanie dla przynajmniej niektórych w∈W – i dzięki temu możemy faktycznie kształtować procesy doboru; patrz kolejna część.) Obliczenia te zależą oczywiście od liczby stanów w świecie oraz od liczby możliwych wartości wypłaty. Odkrywamy jednak dla każdej ze struktur, że w limicie, podczas gdy liczba stanów w świecie i wartości wypłaty ciągnie się w nieskończoność, prawdopodobieństwo homomorfizmów sięga zera.
4. Cztery twierdzenia
Przedstawimy teraz cztery twierdzenia, jedno dla każdej z czterech struktur: całkowitych porządków, grup permutacji, grup cyklicznych oraz przestrzeni mierzalnych. Struktury te odpowiadają percepcji wielkości, takich jak odpowiednio intensywność dźwięku lub ciepło, reorganizacja obiektów, ruchy obrotowe czy przekształcanie przedmiotów w przestrzeni oraz rozkład prawdopodobieństwa. Każde twierdzenie głosi, że prawdopodobieństwo, iż funkcje wypłaty są homomorfizmami struktury jest zerowe. Tym samym prawdopodobieństwo prawdziwego postrzegania każdej struktury spada do zera. Podkreślamy, że twierdzenia te dotyczą samych tylko właściwości matematycznych funkcji wypłaty wynikających z dostosowania. Nie czynią założeń co do – i są całkowicie niezależne od – architektury kognitywnej postrzegającego organizmu, łącznie z tym czy architektura ta realizuje jakiegokolwiek rodzaju wyobrażenia.
W każdym przypadku wyliczamy prawdopodobieństwo zakładając, że istnieją stany w świecie n i możliwe wartości wypłaty m. Następnie pozwalamy n oraz m ciągnąć się w nieskończoność, aby uzyskać wynik.
Obliczanie funkcji wypłaty będących homomorfizmami jest odrobinę skomplikowane; omawiamy je w części przedstawiającej dowody w Załączniku (ich definicje znajdują się w Załączniku A.1). Z kolei wyliczenie całkowitej liczby funkcji wypłaty jest skomplikowane nie jest i dokonano go dla wszystkich czterech twierdzeń. Przedstawimy je poniżej.
Całkowita liczba funkcji wypłaty ze zbioru stanów w świecie NW=n przeniesiona do zbioru wartości wypłaty NV=m to po prostu mn. Powodem tego jest, że każdy stan w świecie może się łączyć z dowolną wartością m, zaś liczbę stanów w świecie wyraża n. Istnieje więc m wartości dla pierwszego stanu w świecie, razy m możliwych wartości dla drugiego stanu w świecie, …. razy m możliwych wartości dla ostatniego stanu w świecie. M zostało pomnożone przez siebie n razy, tj. mn.
Można jednak postawić zarzut, że wyliczenie to obejmuje funkcje wypłaty, które są mało prawdopodobne, takie jak te, w których każdemu stanowi w świecie przypisana jest najmniejsza możliwa wartość wypłaty, W jaki sposób przy tak wadliwej funkcji wypłaty może zachodzić dobór naturalny? Każda strategia będzie ukarana bez względu na to co zrobiła.
Sądzimy, że zarzut ten jest słuszny. Ograniczamy zatem nasze obliczenia do tych funkcji wypłaty, które przyjmują maksymalnie największą możliwą wartość wypłaty dla co najmniej jednego stanu w świecie. Dla takich funkcji wypłaty istnieją strategie, za pomocą których można uzyskać maksymalną nagrodę dla przynajmniej jednego stanu w świecie. Nazywamy je dopuszczalnymi funkcjami wypłaty.
Aby policzyć dopuszczalne funkcje wypłaty, od całkowitej liczby takich funkcji, którą obliczyliśmy powyżej odejmujemy liczbę tych, które nie są dopuszczalne. Funkcja wypłaty nie jest dopuszczalna, jeśli nie przyjmuje maksymalnej wartości wypłaty. Oznacza to, że w najlepszym przypadku przyjmuje jedynie m−1 możliwych wartości wypłaty. Liczbę funkcji od n stanów w świecie do grupy możliwych wartości m−1 można obliczyć stosując tę samą logikę, którą widzieliśmy dwa akapity wcześniej. Liczbą tą jest (m−1)n. Odejmując ją od całkowitej liczby funkcji wypłaty odkrywamy, że liczba dopuszczalnych funkcji wynosi mn−(m−1)n.
Przedstawimy teraz nasze cztery twierdzenia. Pierwsze twierdzenie dotyczy całkowitego porządku. Głosi ono z grubsza, że większość funkcji wypłaty nie jest homomorfizmami całkowitego porządku i dlatego dobór naturalny ogólnie nie wspiera prawdziwej percepcji całkowitego porządku. Bardziej konkretnie mówi ono, że w miarę jak rośnie liczba stanów w świecie i wartości wypłaty, prawdopodobieństwo, że dopuszczalne funkcje wypłaty są homomorfizmami całkowitego porządku spada do zera.
Twierdzenie dotyczące całkowitego porządku
Liczba dopuszczalnych funkcji wypłaty będących homomorfizmami całkowitego porządku wynosi 2(n+m−2m−1). A zatem dla każdej ustalonej wartości m, stosunek dopuszczalnych homomorfizmów całkowitego porządku do dopuszczalnych funkcji wypłaty spada do zera, podczas gdy n ciągnie się w nieskończoność. Dodatkowo, nawet jeśli pozwolimy m rosnąć w takim samym tempie, co n, np. m=n, stosunek ten i tak spadnie do zera.
Dowód. Patrz Załącznik A.2.
Drugie twierdzenie dotyczy grup populacji, które zachowują symetrię. Symetria jest wszechobecna w naszej percepcji, poczynając od rozchodzącej się promieniście symetrii jabłka, przez dwustronną symetrię wielu zwierząt, liści i dzieł rąk ludzkich, aż do bliskiej euklidesowej symetrii przestrzeni wizualnej. Naturalne wydaje się założenie, że owe symetrie postrzegania wiernie przedstawiają symetrie świata, założenie, że[43]:
Symetryczne kształty 3D przedmiotów pozwalają nam nie tylko postrzegać prawdziwie same kształty, ale również w ten sam sposób odbierać rozmiary, ułożenia, kierunki ustawienia i odległości między tymi przedmiotami.
Nasze intuicyjne wyobrażenie symetrii wyraża algebraiczne wyobrażenie grupy[44]. Grupa to zbiór G wraz z działaniem dwuczłonowym, , ∘:𝐺×𝐺→𝐺, które jest łączne ((𝑔1∘𝑔2)∘𝑔3=𝑔1∘(𝑔2∘𝑔3),∀𝑔1,𝑔2,𝑔3∈𝐺), posiada element identyczności (∃𝑒∈𝐺, taki, że 𝑔∘𝑒=𝑒∘𝑔=𝑔,∀𝑔∈𝐺), i każdy element posiada liczbę odwrotną (∀𝑔∈𝐺,∃𝑔−1∈𝐺, tak że 𝑔∘𝑔−1=𝑔−1∘𝑔=𝑒).
Niektóre przykłady grup to rzeczywiste dodawane liczby lub, jeśli pominie się 0, liczby mnożone, grupa Sn permutacji przedmiotów n oraz „pełna grupa liniowa” GL(n) oraz zbiór wszystkich macierzy n×n w działaniu mnożenia macierzy. Innymi przykładami są podgrupy GL(n), takie jak macierze ortogonalne O(n) lub macierze ortogonalne z wyznacznikiem SO(n). W fizyce ważne przykłady podgrup GL(n), gdzie pozwalamy macierzom posiadać skomplikowane wyrazy, to macierze unitarne U(n) oraz macierze unitarne z wyznacznikiem SU(n).
W tym miejscu rozpatrujemy czy funkcje wypłaty są homomorfizmami grup symetrycznych. Grupa symetryczna stojąca ponad każdym zbiorem to grupa, której wszystkie elementy są funkcją wzajemnie jednoznaczną od zbioru do niej samej i której działanie grupowe stanowi skład funkcji. W przypadku skończonego zbioru symboli n, grupa symetryczna Sn składa się ze wszystkich możliwych permutacji symboli n!.
Nasze drugie twierdzenie głosi w przybliżeniu, że większość funkcji wypłaty nie jest homomorfizmami grup symetrycznych, a więc nie postrzegamy symetrii prawdziwie. Ściślej mówi ona, że podczas gdy zwiększa się liczba stanów w świecie i wartości wypłaty, prawdopodobieństwo, że funkcje wypłaty są homomorfizmami grupy symetrycznej spada do zera.
W formule tego twierdzenia liczba stanów w świecie jest taka sama, jak liczba wartości wypłaty, tj. n=m. Jeżeli, jak to zwykle bywa, liczba stanów w świecie przewyższa liczbę tych wartości, możemy uznać, że twierdzenie to dotyczy podgrupy lub podziału n=m stanów w świecie, które charakteryzują się pewną symetrią.
Twierdzenie dotyczące grup permutacyjnych
Liczba funkcji wypłaty będących morfizmami grupy symetrycznej Sn wynosi 2n+n! Zatem ich proporcja do wszystkich dopuszczalnych funkcji wypłaty to 2n+n! przez nn−(n−1)n, którego wartość graniczna wynosi 0 i wyrażona jest jako n→∞.
Dowód. Patrz Załącznik A.3.
Nasze trzecie twierdzenie stanowi kontynuację dociekań na temat symetrii. Przyglądamy się grupom cyklicznym, czyli takim, które może generować pojedynczy element. Jednym z przykładów jest zbiór dodawanych liczb całkowitych Z; w rzeczywistości każda nieskończona grupa cykliczna jest homomorficzna wobec Z. Kolejny wybór przykładów to grupy addytywne Z/nZ, liczby całkowite modulo n; każda skończona grupa cykliczna porządku n jest homomorficzna wobec Z/nZ. Grupy cykliczne pojawiają się na przykład w symetriach obrotowych wielokąta i pierwiastku z jedynki n-tego stopnia (pierwiastek wielomianu xn−1). Grupa rotacji okręgu S1 nie jest cykliczna; nie istnieje rotacja, której moce liczb całkowitych generują wszystkie obroty.
Nasze trzecie twierdzenie głosi z grubsza, że większość funkcji wypłaty nie jest homomorfizmami grup cyklicznych, a więc nie postrzegamy prawdziwie symetrii cyklicznej. Bardziej konkretnie mówi ono, że w miarę jak zwiększa się liczba stanów w świecie i wartości wypłaty, prawdopodobieństwo, że funkcje wypłaty są homomorfizmami grupy cyklicznej obniża się do zera.
Twierdzenie dotyczące grup cyklicznych
Liczba funkcji wypłaty które są homomorfizmami grupy cyklicznej to (m,n), największy wspólny dzielnik m oraz n [45]. Współczynnik liczby cyklicznie homomorficznych funkcji do funkcji dopuszczalnych spada do zera, podczas gdy n ciągnie się w nieskończoność i m≤n.
Dowód. Patrz Załącznik A.4.
Czwarte twierdzenie dotyczy przestrzeni mierzalnych, które zapewniają ramy do opisu prawdopodobieństwa. Rozważmy przykładowo rzut dwiema monetami. Są cztery możliwe wyniki, które możemy zapisać jako X={HH,HT,TH,TT}. Jeżeli monety są uczciwe, prawdopodobieństwo każdego wyniku wynosi 1/4. Mogą nas także interesować skomplikowane zdarzenia, które są podgrupami X. Przykładowo zdarzenie „co najmniej jedna reszka” jest podgrupą {HH,HT,TH}. Jeśli monety są uczciwe, zdarzenie to wystąpi z prawdopodobieństwem 3/4. Przestrzeń mierzalna określa po prostu zbiór możliwych wyników X oraz zbiór 𝒳 możliwych podzbiorów zdarzeń nazwanych X, który uwzględnia wszystkie X, przy czym wymagane jest, aby był zamknięty pod sumą i dopełnieniem, tj. aby był algebraiczny; kiedy X jest policzalny, nazywa się go przestrzenią mierzalną. Tak więc przestrzeń mierzalna to para (X, 𝒳). Jeśli X jest skończony, największa algebra zdarzeń X jest zbiorem wszystkich podzbiorów X, który określa się zbiorem potęgowym X i niekiedy oznacza się jako 2X. Nazywa się to algebrą dyskretną. Najmniejsza algebra zdarzeń składa się z X i jest zbiorem pustym, nazywanym algebrą trywialną.
W przypadku struktur mierzalnych interesujące nas morfizmy to „homomorfizmy odwrotne”. Oznacza to, że jeśli świat posiada strukturę mierzalną (𝑊,𝒲) i wartości wypłaty posiadają strukturę mierzalną (V,𝒱), wówczas interesują nas funkcje f:W→V, dla których f−1 jest homomorfizmem, łącząc elementy V z elementami W. Funkcje takie nazywane są mierzalnymi. Funkcje mierzalne są dla nas interesujące, ponieważ pozwalają, aby prawdopodobieństwa zdarzeń w przeciwdziedzinie informowały o prawdopodobieństwach zdarzeń w tej dziedzinie.
Jeżeli 𝒲 jest dyskretne lub trywialne, albo jeśli 𝒱 jest trywialne, wówczas wszystkie funkcje f:W→V są mierzalne. Jednakże we wszystkich innych przypadkach (tj. tych bardziej związanych z percepcją), nasze czwarte twierdzenie głosi z grubsza, że większość funkcji wypłaty nie jest mierzalnych, a tym samym, że prawdopodobieństwa zdarzeń w naszych doświadczeniach nie informują o prawdopodobieństwach zdarzeń w świecie. Ściślej mówi ona, że w miarę jak zwiększa się liczba stanów w świecie i wartości wypłaty, prawdopodobieństwo, że funkcje wypłaty są mierzalne w odniesieniu do dużej kategorii struktur mierzalnych spada do zera. Każda struktura mierzalna w tej kategorii charakteryzuje się porządkiem k swojej algebry, którym jest minimalna liczba zdarzeń generujących całość algebry poprzez sumę rozłączną. Przykładowo, jeżeli W posiada moc zbioru n, zaś W jest dyskretne, wówczas k=n. Ale jeżeli W jest generowane przez zdarzenia n/2, z których każde zdarzenie zawiera dwa wyniki, wówczas k=n/2.
Twierdzenie dotyczące struktur mierzalnych
Załóżmy, że struktura mierzalna W posiada porządek k i nie jest ani trywialna ani dyskretna. Przyjmijmy ponadto, że struktura mierzalna V nie jest trywialna. Wówczas liczba funkcji mierzalnych jest ograniczona przez mk−1+(m przez m−1)k−1 (m−1)n.
Dla większości wartości k stosunek funkcji wypłaty do wszystkich dopuszczalnych funkcji wypłaty ma wartość graniczną 0, ponieważ n→∞.
Dowód. Patrz Załącznik A.5.
5. Dyskusja: czy dobór naturalny faworyzuje prawdziwą percepcję?
Jest to pytanie techniczne, do którego można się dokładnie odnieść wykorzystując teorię gier ewolucyjnych. W tym miejscu przeanalizowaliśmy funkcje wypłaty gier ewolucyjnych i wykazaliśmy, że ogólnie nie są one homomorfizmami całkowitego porządku, grup symetrycznych, grup cyklicznych oraz struktur mierzalnych w świecie. Dochodzimy do wniosku, że jeśli funkcje wypłaty wymazują te struktury, percepcja i działanie kształtowane przez wspomniane funkcje nie mogą prawdziwie przedstawiać tych struktur ani ich reprezentować. Nasze dowody nie zawierają żadnych założeń dotyczących roli wyobrażeń ani obliczeń w percepcji i działaniu, a więc wynikające z nich wnioski stosują się w tym samym stopniu do każdej algorytmicznej, ucieleśnionej i radykalnie ucieleśnionej teorii percepcji i działania czy też do twierdzenia Bayesa, które zakładają po prostu, że zmysły rozwijają się na drodze doboru naturalnego. Chcielibyśmy omówić listę potencjalnych zarzutów wobec naszego podejścia:
— Stosujemy miarę liczącą, aby udowodnić, że prawdopodobieństwa homomorfizmów są zerowe. Można twierdzić, że jest to niewłaściwa miara. Główny powód zastosowania miary liczącej jest taki, że to uznana bezstronna miara zbiorów skończonych funkcji wypłaty. Zaproponowanie jakiejkolwiek szczególnej, nieobiektywnej miary wymagałoby dokładnego wyjaśnienia dlaczego logika selekcji doboru naturalnego wpływa na tę konkretną, nieobiektywną miarę. Uważamy jednak, że tego zobowiązania nie można wypełnić.
— Wnioski wynikające z naszych dowodów są odporne na zarzut: „nie da się powiedzieć czy coś jest prawdziwe czy nie, jeśli się najpierw nie wie o czym mowa”. Zarzut ten zakłada figuratywne wyjaśnienie percepcji, którego nasz dowód nie wymaga. Co więcej, jest on z gruntu fałszywy: kod poprawiający błędy wykrywa, że otrzymana wiadomość nie jest prawdziwą kopią wiadomości wysłanej, nie znając treści tej wiadomości.
— Można się zastanawiać czy teoria ewolucji może być obiektywnym arbitrem w debacie dotyczącej tego czy dobór naturalny wiąże się z prawdziwą percepcją. W końcu czy ta teoria sama w sobie nie zakłada po prostu prawdziwości określonych postrzeganych przez nas obiektów takich jak organizmy, gatunki, zasoby fizyczne oraz (przy wykorzystaniu jakiegoś testu laboratoryjnego) DNA? Jak teoria ta mogłaby zaprzeczać prawdziwości bez zaprzeczania samej sobie? Dylemat ten ma jednak proste rozwiązanie. Ewolucja na drodze doboru naturalnego – wariacji, selekcji i retencji – posiada algorytmiczny rdzeń, który nie wymaga angażowania DNA, organizmów ani innych tego rodzaju twierdzeń na temat struktury świata. Algorytm ten, spopularyzowany jako „uniwersalny darwinizm”, odnosi się do ewolucji organizmów, ale przypuszcza się, że również do ewolucji sztuki, muzyki, memów, języka oraz instytucji społecznych[46,47].
— Nasz argument opiera się na ewolucji poprzez dobór naturalny. Można postawić zarzut, że na ewolucję wpływa wiele innych różnych czynników – w tym dryf genetyczny, pleotropizm, mechanizm łączący oraz ograniczenia ze strony fizyki i biochemii – i że dobór naturalny odgrywa stosunkowo niewielką rolę.
Jednakże standardowy argument ewolucji na rzecz prawdziwej percepcji głosi, że precyzyjne postrzeganie jest bardziej dostosowane [przydatne], co także stanowi argument na korzyść doboru naturalnego. Zgodnie z naszą wiedzą nie istnieją argumenty przemawiające za prawdziwą percepcją, oparte na dryfie genetycznym, pleotropizmie, mechanizmie łączącym ani ograniczeniach ze strony fizyki i biochemii. Argumenty takie wydają się mało prawdopodobne. Trudno sobie wyobrazić w jaki sposób, dajmy na to, neutralny dryf miałby faworyzować prawdziwą percepcję.
— Nasz wywód skupia się jedynie na czterech strukturach: całkowitym porządku, grupach symetrycznych, grupach cyklicznych oraz strukturach mierzalnych. Istnieje oczywiście wiele innych struktur mających związek z percepcją, takich jak topologie, metryki i częściowe porządki. Struktury te również należy zbadać, aby sprawdzić czy funkcje wypłaty je zachowują. W warunkach idealnych można oczekiwać ogólnego twierdzenia, być może wykorzystującego teorię kategorii i precyzującego wszystkie struktury, które nie są zachowane i tym samym nie postrzegamy ich prawdziwie.
— Można zaoponować przeciwko naszej argumentacji twierdząc, że wiele funkcji wypłaty jest bliskich temu, by je nazwać homomorfizmami struktur świata w sensie, powiedzmy, normy L2 i że z tej przyczyny dobór naturalny tak kształtuje percepcję, że zbliża się ona do prawdziwości, o ile właśnie prawdziwa nie jest. Odpowiadamy, że będą one także bliskie homomorfizmom niezliczonych innych struktur, których nie ma w świecie i dlatego dobór naturalny w taki sam sposób kształtuje postrzeganie tak, by było bliskie innym niezliczonym nieprawdziwym strukturom. Nie ma tu argumentu za faworyzowaniem przez dobór naturalny percepcji bliskiej prawdziwej, a raczej niezliczonych nieprawdziwych możliwości.
Nasze twierdzenia pokazują, że percepcja nie jest prawdziwą prezentacją struktur w świecie, ale czy zamiast tego dowodzą, że stanowi prawdziwy obraz korzyści wynikających z dostosowania? Absolutnie nie. Dobór naturalny znajduje nie idealne, lecz zadowalające rozwiązania problemów adaptacyjnych. Nie muszą być prawdziwe. Staje się to szczególnie wyraźne, jeśli weźmie się pod uwagę, że definicja dostosowania odnosi się wyłącznie do konkurencji modelowanej jako gra (ewolucyjna). Jeżeli tania heurystyka daje większe korzyści niż konkurencja, jest wystarczająco dostosowana [przydatna]. Percepcja nie jest prawdziwa ani w odniesieniu do świata ani do korzyści wynikających z dostosowania. Przypomina raczej interfejs użytkownika [7,18,26,42,48,49]. Interfejs pulpitu ukrywa skomplikowany układ elektryczny komputera. Pokazuje proste ikony, które pozwalają użytkownikowi kontrolować ten układ, mimo że nie ma żadnej wiedzy na ten temat. Oto co uczyniła dla nas ewolucja. Czasoprzestrzeń to nasz czterowymiarowy pulpit, zaś przedmioty fizyczne są ikonami. Nie stanowią prawdziwych obrazów świata. Są interfejsem, który ukrywa świat i kieruje interakcją adaptacyjną w tym ukrytym świecie.
Istnieją dobrze znane przypadki percepcji kodującej korzyści wynikające z dostosowania. Dla przykładu symetria twarzy koduje możliwości reprodukcyjne[50]. Teoria percepcji jako interfejsu głosi, że takie kodowanie jest wszechobecne: czasoprzestrzeń i przedmioty fizyczne są kompresującymi dane i poprawiającymi błędy kodami korzyści wynikających z dostosowania, są zadowalającymi, choć nie idealnymi, rozwiązaniami problemu kompresowania tych korzyści do formatu dającego możliwość działania. Przedmioty fizyczne nie są prawdziwymi obrazami świata, ale strukturami danych, które tworzymy jednym spojrzeniem, zaś pamięć odśmiecamy w mgnieniu oka.
6. Wnioski
Nasza intuicja się buntuje. Przedmioty fizyczne mają silną kontrolę nad wyobraźnią. Trudno jest nam wyobrazić sobie, że widok, zapach i tekstura czerwonej cebuli, które w naszym odczuciu są tak prawdziwe, które odczuwamy tak, jakby przedstawiały rzeczywistość taką jaka jest, są raczej po prostu strukturą danych, którą tworzymy, ponieważ jest to potrzebne do prowadzenia działań adaptacyjnych.
Na szczęście widzimy to jasno na przykładzie synestetyków. Carol Steen dla każdego dźwięku, który słyszy, widzi skomplikowany trójwymiarowy obiekt o wyraźnym kolorze, sposobie poruszania się i fakturze powierzchni. Tworzy ten przedmiot słysząc dźwięk, a następnie niszczy go, kiedy dźwięk milknie. Za każdym razem, gdy słyszy ten sam dźwięk, tworzy ten sam obiekt. Pozwala jej to wyrzeźbić ten przedmiot odtwarzając dźwięk do momentu aż rzeźba zostanie ukończona. Oto jej relacja[51]:
„Te olśniewająco kolorowe i ruchome wizje… przychodzą natychmiast i są wyraźne… Pracuję wykorzystując tylko jeden „impuls wyzwalający zmysł” taki jak dźwięk… słuchanie na raz tylko jednej kompilacji muzyki, odtwarzanej wciąż od nowa dopóki obraz lub rzeźba nie są ukończone. Praca nie musi być skończona w jeden dzień pod warunkiem, że słucham dokładnie tego samego rodzaju muzyki, gdy wracam do przerwanej czynności.”
Michael Watson czuł w dłoniach skomplikowany, trójwymiarowy obiekt za każdym razem, kiedy czegoś smakował. Mięta smakowała jak wysokie gładkie zimne kolumny lodu. Przyprawa do aromatyzowania smakowała jak koszyk bluszczu; syrop Karo jak taca pełna łożysk kulkowych. Watson tłumaczył[52]:
„Kiedy próbuję czegoś o intensywnym smaku, pojawia się odczucie, które obejmuje całą moją rękę od ramienia do czubków palców. Czuję to, co jem – wagę, teksturę, czy jest ciepłe czy zimne, wszystko. Czuję jak bym naprawdę coś chwytał. Oczywiście w rzeczywistości niczego nie ma. Ale to nie jest złudzenie, ponieważ ja to czuję.”
Ewolucja prawdopodobnie nie przebiega z wykorzystaniem interfejsu percepcyjnego Homo sapiens. Nieprzerwanie manipuluje. Tutaj widzimy struktury danych przedmiotów fizycznych, dla których znaleziono nowe zastosowanie w słuchu i smaku. Zastosowanie to jest bezspornie nieprawdziwe. Łożyska kulkowe nie są prawdziwym obrazem syropu Karo; bluszcz nie jest prawdziwą prezentacją przyprawy do aromatyzowania. Przedmioty fizyczne, które normalnie widzimy otwierając oczy nie są niczym więcej jak tymi synestetycznymi obiektami, nieprawdziwymi strukturami danych. Są po prostu zadowalającymi, choć nie idealnymi, rozwiązaniami problemu kompresowania i przedstawiania informacji, dotyczących dostosowania [przydatności] do działania, planowania oraz wnioskowania.
Zobacz na: Nauka spod znaku kultu cargo – Richard Feynman [1974]
Język jako okno na ludzką naturę – Steven Pinker
Koncepcja Czystej Karty [Czysta Tablica/Tabula Rasa] – Steven Pinker
Dysonans poznawczy – Festinger i Carlsmith [1954]
Myślenie pojęciowe, a myślenie stereotypowe – Andrzej Wronka, Kazimierz Ajdukiewicz, Józef Kossecki
Niebieska Pigułka vs Czerwona Pigułka
Bibliografia:
1. Koenderink, J.J.; van Doorn, A.J.; Kappers, A.M.; Lappin, J.S. Large-scale visual frontoparallels under full-cue conditions. Perception 2002, 31, 1467–1475.
2. Koenderink, J.J.; van Doorn, A.J.; Kappers, A.M.; Doumen, M.J.A.; Todd, J.T. Exocentric pointing in depth. Vis. Res. 2008, 48, 716–723.
3. Koenderink, J.J.; Albertazzi, L.; van Doorn, A.J.; van Ee, R.; van de Grind, W.A.; Kappers, A.M.L.; Lappin, J.S.; Norman, J.F.; Stihn Oomes, A.H.; te Pas, S.P.; et al. Does monocular visual space contain planes? Acta Psychol. 2010, 134, 40–47.
4. Masrour, F. The geometry of visual space and the nature of visual experience. Philos. Stud. 2015, 172, 1813–1832.
5. Koenderink, J.J. Color in the Wild; De Clootrans Press: Utrecht, The Netherlands, 2018; Available online: http://www.gestaltrevision.be/pdfs/koenderink/ColourInTheWild.pdf (accessed on 26 April 2020).
6. Logvinenko, A.D. The geometric structure of color. J. Vis. 2015, 15, 16.
7. Hoffman, D.D. Visual Intelligence: How We Create What We See; W.W. Norton: New York, NY, USA, 1998.
8. Koenderink, J.J. Solid Shape; MIT Press: Cambridge, MA, USA, 1990.
9. Koenderink, J.J. About Shape; De Clootrans Press: Utrecht, The Netherlands, 2016; Available online: http://www.gestaltrevision.be/pdfs/koenderink/ShapeTutorial.pdf (accessed on 1 February 2020).
10. Luce, R.D.; Krumhansl, C.L. Measurement, scaling, and psychophysics. In Stevens’ Handbook of Experimental Psychology: Perception and Motivation; Learning and Cognition; Atkinson, R.C., Herrnstein, R.J., Lindzey, G., Luce, R.D., Eds.; John Wiley & Sons: Oxford, UK, 1988; pp. 3–74.
Luce, R.D. A psychophysical theory of intensity proportions, joint presentations, and matches. Psychol. Rev. 2002, 109, 520–532.
Steingrimsson, R.; Luce, R.D. Empirical evaluation of a model of global psychophysical judgments: III. A form for the psychophysical function and intensity filtering. J. Math. Psychol. 2006, 50, 15–29.
Pais, A. Einstein and the quantum theory. Rev. Mod. Phys. 1979, 51, 863–914.
David, M. The correspondence theory of truth. In Stanford Encyclopedia of Philosophy (Fall 2016); Zalta, E., Ed.; Metaphysics Research Lab, Stanford University: Stanford, CA, USA, 2016; Available online: https://plato.stanford.edu/entries/truth-correspondence (accessed on 26 April 2020).
Adelson, E.H.; Pentland, A. The perception of shading and reflectance. In Perception as Bayesian Inference; Knill, D.C., Richards, W., Eds.; Cambridge University Press: Cambridge, UK, 1996; pp. 409–423.
Pizlo, Z. Perception viewed as an inverse problem. Vis. Res. 2001, 41, 3145–3161.
Hoffman, D.D.; Singh, M. Computational Evolutionary Perception. Perception 2012, 41, 1073–1091.
Hoffman, D.D.; Singh, M.; Prakash, C. The Interface Theory of Perception. Psychon. Bull. Rev. 2015, 22, 1480–1506.
Marr, D. Vision; Freeman: San Francisco, CA, USA, 1982.
20. Fodor, J.A. The Mind Doesn’t Work That Way: The Scope and Limits of Computational Psychology; MIT Press: Cambridge, MA, USA, 2000.
21. Pizlo, Z.; Li, Y.; Sawada, T.; Steinman, R.M. Making a Machine That Sees Like Us; Oxford University Press: New York, NY, USA, 2014.
Chemero, A. Radical Embodied Cognitive Science; MIT Press: Cambridge, MA, USA, 2009.
Noë, A.; O’Regan, J.K. On the brain-basis of visual consciousness: A sensorimotor account. In Vision and Mind: Selected Readings in the Philosophy of Perception; Noë, A., Thompson, E., Eds.; MIT Press: Cambridge, MA, USA, 2002; pp. 567–598.
Smith, J.M.; Szathmáry, E. The Major Transitions in Evolution. Oxford University Press: Oxford, UK, 1995.
Michod, R.E. Darwinian Dynamics; Princeton University Press: Princeton, NJ, USA, 1999.
Hoffman, D.D. The interface theory of perception. In Object Categorization: Computer and Human Vision Perspectives; Dickinson, S., Tarr, M., Leonardis, A., Schiele, B., Eds.; Cambridge University Press: New York, NY, USA, 2009; pp. 148–165.
Palmer, S. Vision Science: Photons to Phenomenology; MIT Press: Cambridge, MA, USA, 1999.
Trivers, R.L. The Folly of Fools: The Logic of Deceit and Self-Deception in Human Life; Basic Books: New York, NY, USA, 2011.
Shepard, R. Perceptual-cognitive universals as reflections of the world. Behav. Brain Sci. 2001, 24, 581–601.
30. Churchland, P. Epistemology in the age of neuroscience. J. Philos. 1987, 84, 544–555.
31. Pinker, S. How the Mind Works; W.W. Norton: New York, NY, USA, 1999.
Pinker, S. So how does the mind work? Mind Lang. 2005, 20, 1–24.
Dunbar, R.I.M.; Shultz, S. Evolution in the social brain. Science 2007, 317, 1344–1347.
Nowak, M. Evolutionary Dynamics: Exploring the Equations of Life; Harvard University Press: Cambridge, MA, USA, 2006.
Holland, J.H. Adaptation in Natural and Artificial Systems. An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992.
Prentner, R.; Fields, C. Using AI Methods to Evaluate a Minimal Model for Perception. Open Philos. 2019, 2, 503–524.
Gould, J. The Structure of Evolutionary Theory; Belknap Press: Cambridge, MA, USA, 2002.
Mayr, E. Animal Species and Evolution; Belknap Press: Cambridge, MA, USA, 1963.
Smith, J.M. Evolution and the Theory of Games; Cambridge University Press: Cambridge, UK, 1982.
40. Singh, M.; Hoffman, D.D. Natural selection and Shape perception. In Shape Perception in Human and Computer Vision: An Interdisciplinary Perspective; Dickinson, S., Pizlo, Z., Eds.; Springer: London, UK, 2013; pp. 171–185.
41. Mark, J.T.; Marion, B.B.; Hoffman, D.D. Natural selection and veridical perceptions. J. Theor. Biol. 2010, 266, 504–515.
Hoffman, D.D. The Case against Reality: Why Evolution Hid the Truth from Our Eyes; W.W. Norton: New York, NY, USA, 2019.
Pizlo, Z. Philosophizing cannot substitute for experimentation: Comment on Hoffman, Singh & Prakash. Psychon. Bull. Rev. 2015, 22, 1546–1547.
Reis, C.; Rankin, S.A. Abstract Algebra: Introduction to Groups, Rings and Fields with Applications, 2nd ed.; World Scientific: Singapore, 2017.
Diaz-Vargas, J.; Vargas de los Santos, G. The number of homomorphisms from Zn to Zm. Abstraction Appl. 2015, 13, 1–3.
Dawkins, R. Universal Darwinism. In Evolution from Molecules to Man; Bemdall, D.S., Ed.; Cambridge University Press: Cambridge, UK, 1983.
Dennett, D.C. Darwin’s Dangerous Idea; Touchstone Press: New York, NY, USA, 2005.
Koenderink, J.J. Vision as a user interface. In Proceedings of the Human Vision and Electronic Imaging XVI, San Francisco, CA, USA, 24–27 January 2011.
Koenderink, J.J. World, environment, umwelt, and inner-world: A biological perspective on visual awareness. In Proceedings of the Human Vision and Electronic Imaging XVIII, San Francisco, CA, USA, 4–7 February 2013.
50. Pflüger, L.S.; Oberzaucher, E.; Katina, S.; Holzleitner, I.J.; Grammer, K. Cues to fertility: Perceived attractiveness and facial shape predict reproductive success. Evol. Hum. Behav. 2018, 33, 708–714.
51. Cytowic, R.E.; Eagleman, D.M. Wednesday is Indigo Blue: Discovering the Brain of Synesthesia; MIT Press: Cambridge, MA, USA, 2009.
51. Cytowic, R.E. The Man Who Tasted Shapes; MIT Press: Cambridge, MA, USA, 1993.
53. Robbins, H. A Remark on Stirling’s Formula. Am. Math. Mon. 1955, 62, 26–29.
54. Rotman, J. Galois Theory; Springer: New York, NY, USA, 1998.
55. Morandi, P. Automorphisms of Sn and of An; Lecture notes; New Mexico State University: Las Cruces, NM, USA; Available online: https://wordpress.nmsu.edu/pamorand/mathematical-notes/ (accessed on 27 April 2020).

Najnowsze komentarze